Violation of assumptions, or are your migration estimates wrong when the populations split in the recent past?
August 15, 2010
When do we get fakes, or did you ever wonder whether MIGRATE-N gives you wrong results because your data was sampled in populations that separated only recently? I am sure many worry about this, because many MIGRATE-N users ask me about this topic.
In the last few days, I experimented with different population splitting times and recorded how MIGRATE-N reports migration rates. I used BayeSSC (Anderson et al 2005, Excoffier et al. 2000) to generate the data (if you are interested to see all the files: parameter files, infiles, parmfiles, and outfiles, get the compressed archive [no ready yet]).
I generated 15 datasets for 40 haploid chromosomes (20 diploid individuals) from two populations, for each individual 10 loci with 1000 bp were scored. This analysis is certainly not a full scale simulation study but indicates the behavior of MIGRATE-N with data that violates the assumptions of the methods to a various degree. The coalescent suggests that in a single population we expect to have all lineages coalesce after about 4Ne generations looking into the past (for mtDNA in diploids with equal sex-ratio this would be Ne generations), such a rational suggests that a population genetic models that only allow the transfer of genetic material between populations through migration events work for datasets that either had populations that split long time ago or then are very small. The 15 datasets were using population splits at 1250 (Ne/2) , 2500 (Ne), 5000 (2Ne), 10000 (4Ne), and 40000 (8Ne) generations, using a combined effective population size of 5000 (diploid organism).
-
-Five datasets had no migration between the populations after the split.
-
-Five datasets used a symmetric migration model after the split using migration rates of m=0.000025; this is equivalent to an M=100 when the population size Theta is 0.0025.
-
-Five datasets used a symmetric migration rate of m=0.00025, which translates to M=1000.
Therefore, I explored effects on the estimation of migration rates in situations where the assumptions of MIGRATE-N are certainly violated.
MIGRATE-N estimates mutation-scaled migration rates for the 5 datasets without migration, because MIGRATE-N does not estimate a split time all migration rates will be either zero or inflated. I report here the 95% credibility interval and the mode of the posterior distributions of short runs of MIGRATE-N 3.1.8 using program defaults. The program settings should be probably improved, but despite the short runs the results show the trends clearly.
The Table 1 shows clearly that even with rather recent population splits rejection of the zero migration rate is difficult and only the population split 1250 generations ago allows a clear rejection of a zero migration rate. Table 2 shows the values for the simulations where there is some migration after the population split. Again, only the very recent split does not include the true mutation-scaled migration rate of 100.
Table 3 shows that with higher migration rate, even with low divergence values the true migration rate values are in the credibility set for all the population splits tried. It is striking that in all trials the population sizes respond very lottle to the changes in divergence times.
I also ran a set of simulations with M=10000, but I have difficulties to get decent migration rate values for the deep splits (40000 and 10000 generations ago). The migration estimates are too low for those (about 5x too low) and the estimates of the 1250, 2500, and 5000 generation splits include the truth. I will amend the blog once I am clear on the the bias of the splits that are long ago.
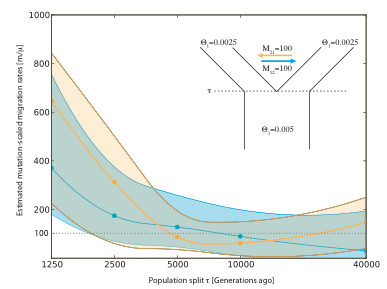
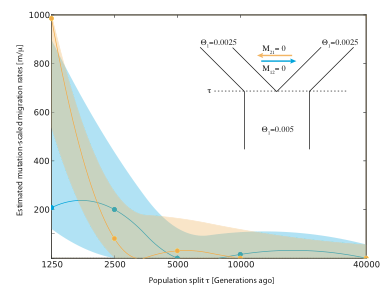
It would be very interesting to see how powerful programs like IM/IMa are to detect these recent divergence time and what the estimation of migration rates are.
One last note, the simulations were done with a particular setting of population sizes, we should think in fractions of the effective populations size:
For 2-population scenarios: If you are worried about the accuracy of the migration rates and want to take the migrate rates literally, then the Divergence time should be larger than the effective population size of the subpopulations, or larger than a half of the total population With high migration rates even more recent divergences may be tolerable.
Citations:
Anderson CNK, Ramakrishnan U, Chan YL and Hadly EA (2005) Serial SimCoal: A population genetic model for data from multiple populations and points in time. Bioinformatics, 21, 1733-1734.
Excoffier L, Novembre J and Schneider S (2000) SIMCOAL: a general coalescent program for simulation of molecular data in interconnected populations with arbitrary demography. J. Hered., 91, 506-509.
Greta Pratt. (2005) Nineteen Lincolns, 18 archival inkjet prints. The Old, Weird America: Folk Themes in Contemporary Art (2009). Decordova Sculpture Park -- Museum , Lincoln MA. (Photo PB)
