You have it all backwards!

or

Why is population genetics so confusing

Peter Beerli 2013

I get often asked about the precise meaning of parameters in my program migrate because some researchers give confused advice about what backwards and forwards migration really means in general and in particular for migrate.

If you are short-tempered here the conclusion: migrate uses backward migration rates like any other population genetics method out there, for example, Nm in migrate has the same meaning as Nm in the context of FST.

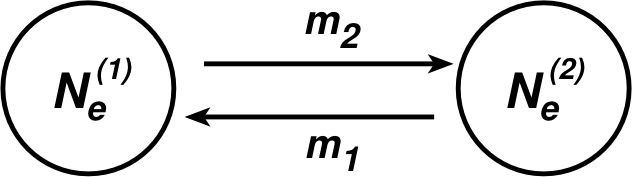
Let’s consider a simple two-population model, we could use four parameters for a neutral model and specify the number of individuals in in population 1 as Ne(1)  and the number of individuals in population 2 as  Ne(2) with migration rates m1  and and m2, we define: 

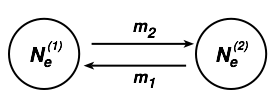
“m is the migration rate, the fraction of individuals in a population that is composed of immigrants. More precisely, m is the backward migration rate. It’s the probability that a randomly chosen individual in this generation came from a population different from the one in which it is currently found in the preceding generation. Normally we’d think about the forward migration rate, i.e., the probability that a randomly chosen individual will go to a different population in the next generation, but backwards migration rates turn out to be more convenient to work with in most population genetic models.” [citation from Kent Holsinger’s excellent population genetics text http://darwin.eeb.uconn.edu/eeb348/lecturenotes/mutation-drift.pdf ]. Just in case that you think that Kent and I are weird, this is the standard definition Sewall Wright used: backwards is used because we think of past immigrants and not of emigrants. For most if not all population genetics inference, we could not care less how many random individuals leave a population because whether they arrive at another location or die trying is irrelevant for the source population, but if they arrive at a new location they can have an effect and change the allele frequencies at the new location.

To summarize: migration in population genetics is always expressed as the fraction of immigrants in population i that came from population j in the last generation; perhaps we should start to call it the immigration rate. The definitions above for m2 could be expressed as m1→2, because the two populations represent the whole world.

migrate expresses its parameters scaled by the mutation rate because when using genetic data form a single time point we are not able to separate the influence of mutation µ (mu) and population size, thus we use the product of the two and have the mutation-scaled effective population size Q which is 4Neµ and the mutation-scaled immigration rate M which is m/µ.  migrate estimates these parameters and presents them in tables and posterior distributions, to summarize the relationships look at this (for the immigration into population 1 and size of population 1):

The inheritance scalar x is usually 1 for mtDNA data extracted from vertebrates with with a fixed gender through their lifetime and a 1/1 sex ratio, and is 4 for nuclear markers.  The confusion about backwards and forwards increases if we consider a coalescence framework.  Coalescence theory is a framework in population genetics that allows calculating probabilities of particular genealogies (relationships of sampled individuals) given the number of samples and the population size of the whole population.

For example here is a Wright-Fisher population of size 30 with 10 randomly sampled individuals (see inset graph [created with a python program that you can download from http://people.sc.fsu.edu/~pbeerli/programs/popvizard.tar.gz]). If we extend this framework to multiple populations then we have to work with the structured coalescent where we consider not only coalescent events (internal nodes on the tree where two lineages join) but also switches of the population state along the genealogy. Usually this is achieved by inserting a migration event.  The calculation of the probability becomes more involved because we need now track 4 different types of events (coalescence in population 1, coalescence in population 2, immigration into 1, and immigration into 2. This is done backwards in time by calculating the probability that a particular line in population i is a forward-in-time descendent from population j using the Wright-Fisher interpretation of immigration.

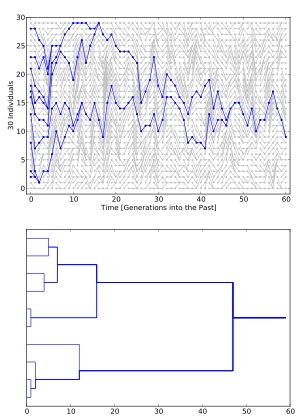
Sometimes you may be told that because it is a coalescent framework it is backward (or forward) migration, this is not correct.  A migration event at time t, forces the change of the population label, looking forward in time the label was x at t-∂ and at t it will y. The placement of these events depends in the backward immigration rate (see part one) into y and the number of lineages that are in y, but the event itself has no time component and is neither forward or backward in time. Of course, it is true that before the migration event the sample lineage was in a different population, but this does not mean the risk of switching populations is dependent on the past location of the same lineage.

Peter Beerli

March 2013